二分搜索树BST、AVL树
二分搜索树(Binary Search Tree)
相比于二叉树有更加严格的性质:
- 无重复元素
- 从左到右、从上到下依次增大
寻找(Find)
核心想法是一直比较左右节点,然后向下递归查找。
- 找最小
1 2 3 4 5 6 7
BinaryNode<Comparable>* findMin(BinaryNode<Comparable>* t) const { if (t == nullptr) return nullptr; if (t->left == nullptr) return t; return findMin(t->left); }
- 找最大
1 2 3 4 5 6 7
BinaryNode<Comparable>* findMax(BinaryNode<Comparable>* t) const { if (t != nullptr){ while (t->right != nullptr) t = t->right; } return t; }
- 找任意一个
1 2 3 4 5 6 7 8 9 10
bool contains(const Comparable& x, BinaryNode<Comparable>* t) const { if (t == nullptr) return false; else if (x < t->element) return contains(x, t->left); else if (t->element < x) return contains(x, t->right); else return true; }
时间复杂度都是 $O(h)$ 。
插入(Insert)
插入节点只插在叶子节点后
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void insert(const Comparable& x, BinaryNode<Comparable>*& t)
{
if (t == nullptr)
{
t = new BinaryNode<Comparable>(x, nullptr, nullptr);
}
else if (x < t->element)
{
insert(x, t->left);
}
else if (t->element < x)
{
insert(x, t->right);
}
else
{
; // Duplicate, do nothing
}
}
移除(Erase)
分为三种情况:
- 叶子节点
delete然后其父节点的相应子节点设为nullptr - 该节点有一个子节点 子节点接到父节点,删除该节点
- 该节点有两个子节点(Full Node) 选左子树最大/右子树最小,替换该节点,删除该节点(可能会用到前两种情况)
要对原树进行操作,需要传入引用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void remove(const Comparable& x, BinaryNode<Comparable>*& t) {
if (t == nullptr)
return; // Item not found; do nothing 未找到
if (x < t->element)
remove(x, t->left);
else if (x > t->element)
remove(x, t->right);
else if (t->left != nullptr && t->right != nullptr) // Two children 两个子节点
{
t->element = findMin(t->right)->element; // 找到右边最小的
remove(t->element, t->right);
}
else // 回到前两种 remove
{
BinaryNode<Comparable>* oldNode = t;
t = (t->left != nullptr) ? t->left : t->right;
delete oldNode;
}
}
前驱/后继(Predecessor/Successor)和找到第 k 个元素
也可以理解为前一个小的,后一个大的;以及查找第 $k$ 个,$k$ 是从1开始的索引;
对于如何找到第 $k$ 个元素,这里有一个关键的前提,树中的每个节点必须额外存储该节点(及其所有后代)的总大小 (tree_size) 。由于是递归的查找,所以都是从根节点开始。
假设我们获取了左子树的大小为 $l$ :
- 若 $l=k$ :那么左子树正好有 个元素(索引从 0 到 $k-1$)。此时当前节点就是我们要找的索引为 k 的元素。
- 若 $l>k$ :左子树的元素数量大于 $k$ ,也就是第 $k$ 个元素在左子树中。需要我们在左子树中递归地查找第 $k$ 个元素。
- 若 $l<k$ :不在左子树,也不是根节点,在右子树。我们已经在左子树中跳过了 $l$ 个元素,并跳过了 1 个根节点。因此,我们现在需要寻找的目标在右子树中是第 $(k - l - 1)$ 个元素。递归地在右子树中寻找第 $(k - l - 1)$ 个元素。
对于寻找前驱和后继,其逻辑是镜像对称的,这里用寻找后继来举例解释:
寻找后继节点分为两种情况:
节点有右子树 : 后继节点是其右子树中“最左边”的节点,也就是右子树中的最小值;
节点没有右子树 : 想象一下,这个节点的后继应该是向上搜索的过程中,第一次向右边走到的父节点,可以称为“最低的祖先节点”,这个最低的祖先节点的左子树包含了当前节点。
需要注意: 在情况2中,如果一直向上遍历到根节点却依然处于该父节点的右子树,那么就说明当前节点就是一整颗树的最大值!没有后继!
这部分内容先写到这(PPT上也就这些内容了),脑子有点不够用了,判断这些边界,特别是索引和个数混在一起的实在是太勉强我了。
时间复杂度分析
- 最坏的情况是 $O(n)$ ,这个 BST 变成一个链表
- 最好的情况,PerfectBST,$O(ln(n))$
- 我们的目标是让这个树的高度维持在 $\Theta(ln(n))$
一个随机生成的二叉搜索树的平均高度实际上是 $\Theta(\ln(n))$ ;但是在随机插入和删除之后,平均高度倾向于增加到 $\Theta(\sqrt{n})$。
那么如果我们希望能保持比较好的情况的话,我们需要让这棵树满足一定的性质, 这棵树需要是平衡的(Height Balanced),事实上一棵树的平衡属性有很多,可以是权重平衡,也可以是高度平衡,为了实现我们上述的要求,需要的应该是能实现高度(深度 Depth)平衡的。
AVL Tree
AVL 树是实现高度平衡的良好实践。
平衡的概念:任意一节点的左右子树高度差 $\leq 1$
最简单的不平衡情况
首先我们来考虑一种最简单的不平衡的情况,这三个节点如何将不平衡调整为平衡是后续更加复杂的平衡性修正的基石。
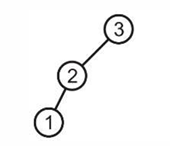
- 第一种最简单情况:
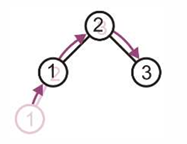
3的左子树和右子树的高度差是2 $\geq$ 1,不是平衡的,不平衡现象发生在节点3。 修正的方法也很简单,只需要将2这个中间大的元素移动为根节点即可,这样能满足左右节点的大小要求。
这样调整完根节点之后这个树就重新变为一个平衡的树了。
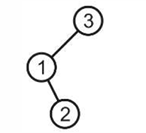
- 第二种最简单情况:
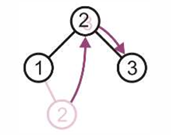
但是如果我们仍旧采用第一种情况的解决办法,那么1的左子树就是2,但是2是比1大的,不符合二分搜索树对于左右节点大小的要求。
此时的修正方法是这样的:
了解了这两种情况更加有利于后续复杂情况下的修正。
通用的修正方式
具体步骤:
- 先判断哪个节点是发生不平衡的地方,注意这个不平衡子树的路径;
- 从这个不平衡的点沿路径向下构建前面说的三个点的最简单情况
- 判断这个不平衡的类型是什么样的,具体有:
- 修复(可能需要多次)
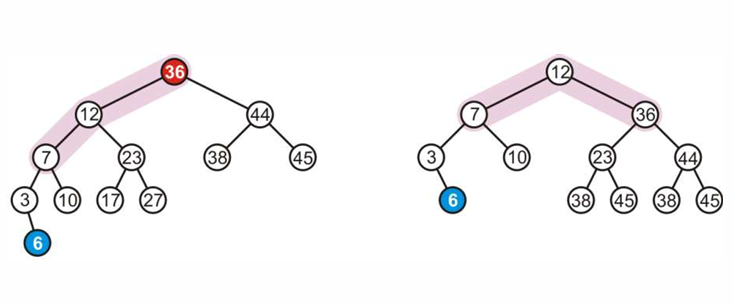
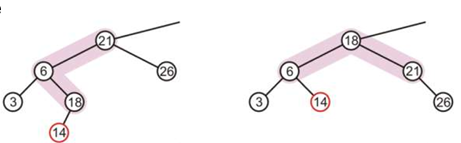
来看两个 LL 和 LR 的例子:
LL :高度发生不平衡的节点是36
LR :高度发生不平衡的节点是21
至于 RR 和 RL 另外两种,只是上面两种的镜像形式,操作都是一样的。 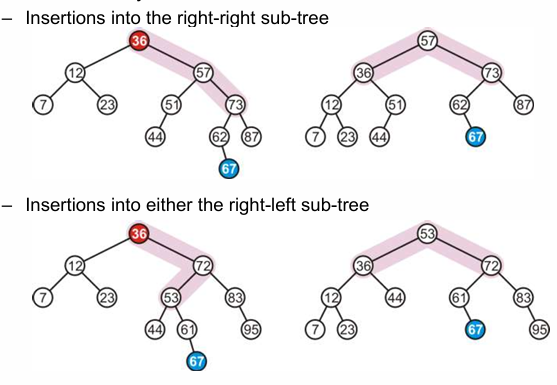
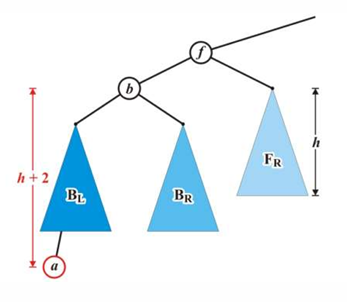
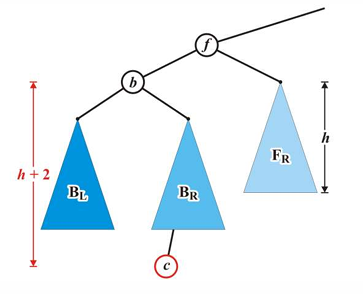
不平衡的情况通常发生在 insert 和 erase 操作时,因此若在一个平衡的树中进行插入则必须要判断并修复;一般来说,insert 至少都要一次修复,而erase可能需要 $O(h)$ 次修复。
insert 和 erase 的演示 P156-P203