多路树和B+树

学习完二叉树和二分搜索树之后我们可以再来看看三叉树是怎么实现的，随后可以推广到多叉树。

三叉树

三叉树的一个节点需要两个值和三个指针，以及一个 int num_values (1 or 2) 来存储当前节点有几个值（还有几个空位）。

这是因为为了实现三叉树，必须要有两个可进行比较的元素来将当前进入的节点划分到两个值切成的三个范围中（也就是三个指针指向左、中、右子树）。

和二叉树的本质是一样的（一个值分出两个区域）。

更多三叉树的操作不一一列举，可自行查找资料和看 P7-10

关于三叉树的 insert 操作和上面讲的并无差别，简单来说就是：P11

• 先尝试进入当前节点中，并按照值的大小来进行排列；
• 节点若满，则和节点中的两个值进行比较并前往左、中、右子树；

三叉树中序遍历（In-order Traversal）

关于中序遍历，可以先看看二叉树的中序遍历，在Leetcode上有这么一题。 二叉树的中序遍历就是按照左子树，右子树来进行递归遍历。

三叉树中序遍历的具体实现：

template <typename Type>
void Three_way_node<Type>::in_order_traversal() const {

    if (!full()) {
        cout << first();
    } else {
        if (left() != nullptr) {
            left()->in_order_traversal();
        }
        cout << first();
        if (middle() != nullptr) {
            middle()->in_order_traversal();
        }
        cout << second();
        if (right() != nullptr) {
            right()->in_order_traversal();
        }
    }
}

我们当然可以拓展到N叉树（N-ary Tree）的中序遍历，代码实现也是一样的思路，我们可以使用一个循环来进行中间多个值的中序遍历操作：

template <typename Type, int N>
void Multivay_node<Type, N>::in_order_traversal() const {
    if (empty()) {
        return;
    } else if (!full()) {
        for (int i = 0; i < num_values; ++i) {
            cout << elements[i];
        }
    } else {
        for (int i = 0; i < N - 1; ++i) {
            if (subtrees[i] != nullptr) {
                subtrees[i]->in_order_traversal();
            }
            cout << elements[i];
        }
        if (subtrees[N - 1] != nullptr) {
            subtrees[N - 1]->in_order_traversal();
        }
        
        subtrees[N - 1]->in_order_traversal();
    }
}

多路树的高度和规模（Size of Multiway-Tree）

现在我们可以来看看多路树的高度和规模问题。

• 高度为 $h$ 的完美多路树中节点的最大数量为 $N^{h+1} - 1$ ，当 $N = 2$ ，这个就变成了二叉树中的计算方法。
• 同样地，我们可以从另一个角度来看，对于完美多路树，如果每个节点都是满的，即每个节点都有 $N - 1$ 个值，那么总共就有 $\frac{N^{h+1} - 1}{N - 1} (N - 1) = N^{h+1} - 1$ 个。得到的结果和上面是一样的。

除此之外，我们还需要注意到：在完美二叉树中，叶子节点比上面全部节点多一个。那么在多路树中还是这样的吗？

对于一个高度为 h 的完美 N 路树，它有 $N^h$ 个叶子节点，每个叶节点存储 $N−1$ 个元素，计算出叶子节点存储元素占总节点数的比值：\(\frac{N^h \left( N - 1 \right)}{N^{h+1} - 1} \approx \frac{N^h \left( N - 1 \right)}{N^{h+1}} = \frac{N - 1}{N}\) 由此，可以发现一个多路树（$N>=2$）中，大部分元素（值 / value）是位于叶子节点的。

• 在 8 路搜索树中，约 87.5% 的元素位于叶节点中；
• 在 100 路搜索树中，约 99% 的元素位于叶节点中；

至此，我们可以发现：

• 多路树在从根节点到叶子节点（或树中的节点）时有着更短的路径；
• 多路树的实现和节点之间的移动更加复杂；
• 当在节点之间进行移动或搜索的成本巨大时，多路树通过减少树的高度可以高效规避这个问题的产生。

B+树

为了更好的了解，先回顾一下存储容量单位对比：

十进制单位 (SI 前缀)	关系式	二进制单位 (IEC 前缀)	关系式	换算成字节
$1 \text{ kB}$	$= 1000 \text{ bytes}$	$1 \text{ KiB}$	$= 2^{10} \text{ bytes}$	$= 1\,024 \text{ bytes}$
$1 \text{ MB}$	$= 10^6 \text{ bytes}$	$1 \text{ MiB}$	$= 2^{20} \text{ bytes}$	$= 1\,048\,576 \text{ bytes}$
$1 \text{ GB}$	$= 10^9 \text{ bytes}$	$1 \text{ GiB}$	$= 2^{30} \text{ bytes}$	$\approx 1.073 \cdot 10^9 \text{ bytes}$
$1 \text{ TB}$	$= 10^{12} \text{ bytes}$	$1 \text{ TiB}$	$= 2^{40} \text{ bytes}$	$\approx 1.100 \cdot 10^{12} \text{ bytes}$

在计算机中，不同的数据存储单元访问时间各不一样：

• 缓存（Cache）：1GHz
• 内存（Main memory（SDRAM））：100MHz
• 硬盘（Hard drive）：100Hz

相比于缓存和内存，硬盘的数据访问速度非常的缓慢。

除此之外，内存是 byte addressable （字节寻址） 的，也就是如果想要访问一个 bit，就需要先找到其所在的 byte。 但是对于硬盘却是 block addressable （块寻址），假设一个“块”占用 4KiB，那么访问一个 bit 就需要加载一整个块，这样I/O效率是及其低下的。

并且文件存储占用的是整数个块，容易出现一个块用不完的情况而造成空间浪费，这也是为什么当我们查看一个文件时，其文件大小和占用空间是不一样的。

此时假如我们需要存储 $10^9$ 的条记录，使用二叉搜索树的话，需要走的树的高度就是 $lg(10^9)\approx29$ ，硬盘每次寻找需要10ms，那么这样一次寻找就需要 0.29s，时间花费非常长。

那么此时我们就可以考虑采用多路树来降低树的高度，从而加快寻址。

假如此时需要存储大量的键值对记录，一个 key 为 4 byte，一个 value（一般为指针）为 4 byte，那么一个4 KiB的块就可以存储512个键值对，可以使用 512路树。 此时多路树的高度下降到 $log_{512}(10^9)\approx3$ ，搜素时间变为30ms，这是非常大的改进！

如果我们希望节点中还能存储100 bytes 的数据信息呢？此时一条记录的大小就是 108 B，那么一个 block 中能存储的记录减少为37条，可以采用 38路树。

现在让我们再次回顾一开始的目标是什么。

• 我们希望能降低硬盘中数据搜索的时间，加快速度，那么就是需要更低的多路树的高度。
• 我们还希望能尽可能提高每一个块存储的数据量，那么就是需要更多的节点中的值。

还记得前面我们说到多路树大部分元素都是存储在叶子节点中吗？

如果我们只使用叶子节点来存储那 100B 的数据，剩下的全部用来存储负责寻址的键和指针，那么好像就能实现上面两个要求的充分平衡了！

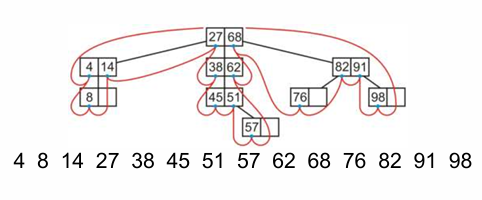
B+树可以看成：内部节点块（用于寻址）+叶子节点块（存储数据）

红色区域就是叶子节点块

现在我们来算算，4B 的 key 和 100B 的数据构成叶子节点，那么用于储存数据的 block 就有 $ \frac{4KiB}{104B/record}\approx 39records$

那么 $10^9$ 条数据记录需要 $10^9/39=25641026$ 个叶子节点块；

一个 block 全部用于存储负责寻址的键值对的话可以存 512 条记录。

一个512路树可以存储 $512^{h+1}$ 的节点，那么负责寻址的这个树高度为 $h=log_{512}25641026-1=2$ ，加上叶子节点链接到记录数据的一层，高度就是 $3$ 。

但是通常各个节点并不会是满的，现在定义 $M$ 路树，每个叶子节点块可以储存 $L$ 条记录。

• 最好情况：$M=512,L=39$，全满。高度为：$h = \left\lceil \log_{512} \left( \frac{10^9}{39} \right) \right\rceil = 3$
• 最差情况：$M=256,L=20$，都半满。高度为：$h = \left\lceil \log_{256} \left( \frac{10^9}{20} \right) \right\rceil = 4$ 如果要存 $10^{13}$ 条数据的话，最好和最差高度都是 $5$。

至于为什么最差是半满？B+树有一个强制性的规则来保证节点不会过空。 暂时简单理解为小于半满的两个兄弟节点会发生合并。

可以看出在大量数据访问时，B+树的稳定性是很好的。

通过B+树访问时，时间复杂度都是 $\Theta(ln(n))$，因为必须要寻找到叶子节点。

B+树具体寻址，P103

后续以及B+树的 insert，erase操作，如何继续分裂节点？

insert 看要插入的节点和当前比较节点的大小，$\geq 87$ 则分配到 87 所在数据块处。