最小生成树MST及其构建算法、最短路径算法

发表于 2025/12/01 更新于 2025/12/31

作者 CrabPeelMyShell

35 分钟阅读

生成树 Spanning Tree

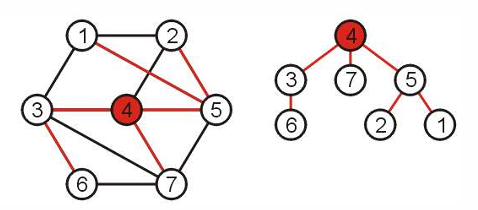
给定连通图中的 $|V|=n$ 个节点，使用 n-1 条边将这些点连接起来。在这些点中选取一个根节点，即成为一颗生成树。生成树不是唯一的，可以选取不同的顶点作为根节点。

生成树可以很奇特：

最小生成树 Minimal Spanning Tree

如果我们将这个图的边添加权重，那么所包含的边权重最小的生成树就是最小生成树。对于没有显式给出权重的图，我们可以认为连通的边权重为1，未连通的边权重为0。

多个最小生成树组成的集合就是一个最小生成森林。

根据最小生成树的定义，假设当前随机给出一个顶点。要想实现最小生成树，需要考虑它的全部邻居，并且找到一个节点，它和当前节点连通的边的权重是所有邻居当中最小的（距离最近的），连到当前节点。

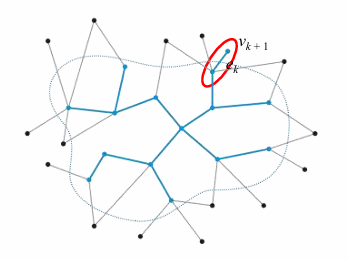
假如此时已经有一个部分构建好的最小生成树，把它看成一个超级顶点，那么需要考虑的就是这个超级顶点的全部邻居连通的边，找到最小的那个。如图中的边 $e_k$ 和顶点 $v_{k+1}$ 。

关于为什么始终要连接权重最小的这个边，可以使用反证法去验证（在直觉上这可能是成立的），在此不赘述。 P136

Prim 算法构建最小生成树

关于最小生成树的构建，Prim 算法给出了相似的步骤：

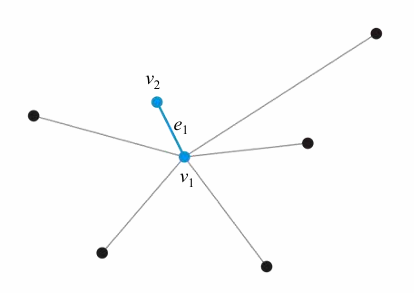
随机选取一个顶点作为MST构建的开始节点（$v_1$）；
选择一个和当前MST距离最近（$e_1$）的一个邻居顶点（$v_2$）进行连接；
如果仍有未被访问的顶点，继续迭代：
- 选择和当前MST距离最近且未被访问的邻居；
- 将这个邻居（$V_i$） 标记为已被访问（连入当前MST）；
- 检查 $V_i$ 的未被访问的邻居，如果现在连通边的距离是更小的，那么
  - 将未被访问的邻居顶点到 $V_i$ 的距离（也就是到MST的距离）更新为现在更近的这个距离；
  - 将 $V_i$ 设为其邻居的parent；

在这个过程中需要始终注意的是：当我们选择了距离当前MST最近的邻居顶点（$V_i$）后，需要更新的是 $V_i$ 的邻居顶点的distance和parent状态。

选择最近的顶点是对于MST（整个表）来说的，可能需要更新的邻居顶点是对于新加入的这个顶点（$V_i$）来说的。

使用 Prim 算法构建MST时，需要先构造3个数据：

一个布尔值，用于标记某个顶点是否连接到了当前的MST；
当前MST（超级顶点）和某个邻居连接的边的权重（看作距离distance）；
某个邻居和当前MST中的哪个顶点相连（像一个指针，指向parent）；

这三个数据都可以通过array/vector来存储，初始化需要 $\Theta(|V|)$ 的时间和空间复杂度。

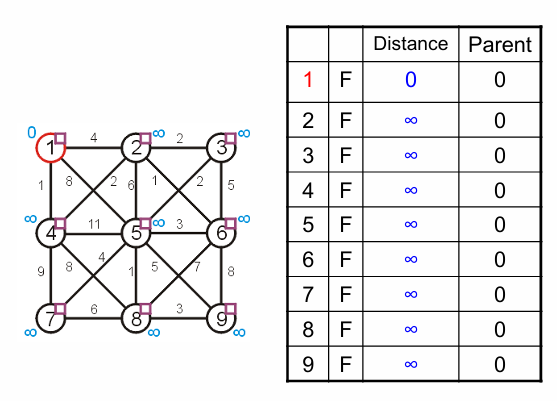
然后将数据初始化：（见下图）

随机选择一个根节点并将其distance设为0，其余全部节点的distance设为 $\infty$ ；
全部节点都设置为未被访问（未连接到MST）；
顶点和MST中相连的顶点（parent）编号为0（没有和MST中的顶点连接）；

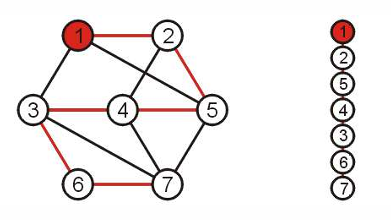
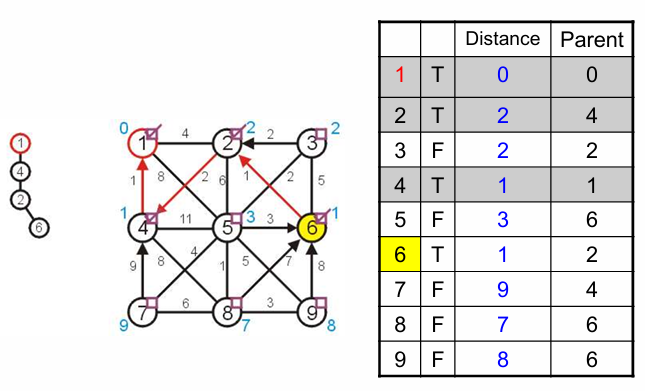
首先选取顶点1作为根节点：（P150-167）

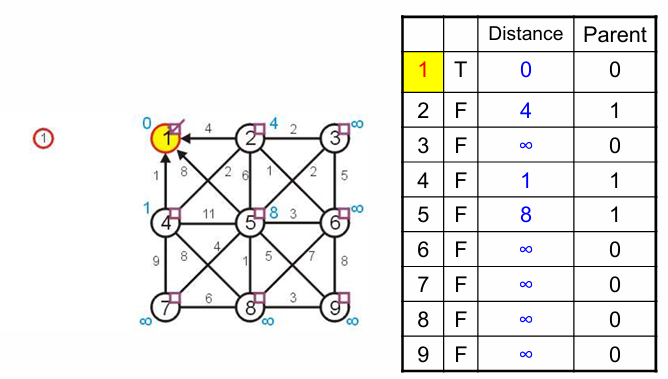
将顶点1加入MST，更新1的状态和1邻居的状态：

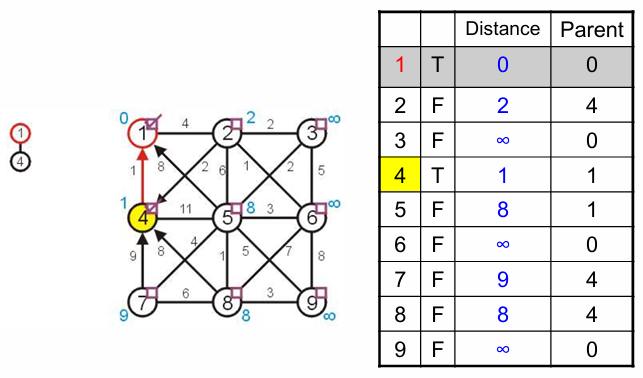
在1邻居中挑选未被访问且distance最小的邻居连接，即4，并更新4及其邻居的信息；

注意这里不能更新5的distance，5和当前MST连接的顶点是1，distance=8，小于和4相连的distance=11，因此parent仍指向1；

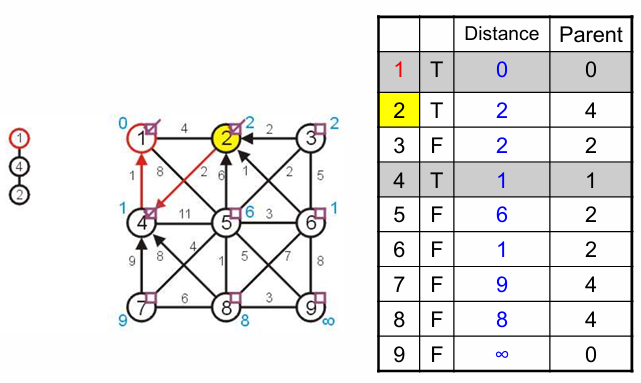
在4的邻居中挑选未被访问且distance最小的邻居连接，即2，更新2及其邻居信息；

此时需要更新5的distance，因为5连接到当前MST的顶点（2号）距离最近，小于连接到1、2、4的distance。

在12的邻居中挑选未被访问且distance最小的邻居连接，即6，更新6及其邻居信息；

此时5的信息又被更新了，连接到当前MST顶点（6号）的distance更小，小于之前的6号distance=6。并且8号的信息也被更新，比之前和4号相连的要小。

不断进行下去，直到没有未被访问的顶点，构建完成最小生成树。可能会有顶点无法连接上，那就说明该MST是当前图$G$的一个连通子图$G_{sub}$，但这个图$G$不是一个连通图。

在上面的这个过程中，我们需要不断地遍历这个列表来不断更新当前MST的全部邻居并找到距离最近的那个顶点然后连接。但是我们每一次的访问总会减少一个未被访问的顶点，所以Prim算法尽可能地将需要访问的顶点数降到了最低。

Prim 时间复杂度分析：

1、首个顶点是随机选取的，需要再遍历 $|V|-1$ 个顶点才能构建，那么就需要 $\Theta(V)$ 的时间；

2、在上面遍历每个顶点的过程中，

为了找到距离最小的未被访问的邻居，还需要遍历整个表，花费 $\Theta(V)$ 的时间；
每当我们遍历完整个表，找到一个符合要求的邻居顶点，将其连入后还需要考虑他的全部邻居，因为我们还要判断他的全部邻居顶点有没有被访问过？如果没有，需不需要更新更短的距离？

但是现在，回顾一下前面提到的邻接矩阵和邻接表，我们发现这两种不同的表示形式会对这一步花费的时间产生不同的影响。

对于邻接矩阵，给定一个节点，找它的邻居节点并判断要不要更新需要 $\Theta(|V|)$ 的时间；这样，总的时间复杂度就是 $\Theta(|V|(|V|+|V|))=\Theta(|V|^2)$
对于邻接表，每一个节点的后面跟着的邻居节点链表长度平均为 $\frac{|E|}{|V|}$ ，给定节点的邻居节点查找并判断是否要更新需要 $\Theta(\frac{|E|}{|V|})$ 的时间；这样，总的时间复杂度就是 $\Theta(|V|(|V|+\frac{|E|}{|V|}))=\Theta(|V|^2+|E|)$ ，而 $|E|=O(|V|^2)$ （在前面无向图的部分有提到），因此最终还是为 $\Theta(|V|^2)$ 。

到这里，我们总是会继续发问，还能更快吗？

来一步步看看哪里还有改进的空间。

主循环需要遍历完 $|V|-1$ 个节点，这里我们没法再压榨出时间了；

每个循环中，我们需要找到距离最近的那个邻居节点，这其实很像一个排序问题，需要找到那个最小的元素。但我们学习过的排序算法最快也是 $O(n)$ 的时间，而且稳定的都是 $O(nlog(n))$ 的，好像让Prim变得更糟了。

再仔细想一下，这其实也可以看成是一种优先队列，毕竟我们一直要的只是距离最小的那个，并不对后面元素的顺序做出多么苛刻的要求。那么用堆（Min-Heap）来实现不失为一个很好的选择，这里需要用到的堆的操作（push，insert，上下滤）都是和堆高有关，也就是 $O(log(n))$ ，在这里我们找到了继续压榨时间的可能。

然后再看，当我们添加了一个距离最近的邻居节点后，还需要遍历他的邻居节点并判断是否需要更新distance和parent。这里我们仍旧没有办法压榨时间。

所以我们在这里就需要考虑如何使用堆来加速距离最近的节点的查找。

使用邻接矩阵，遍历新加入的最近的邻居节点还是需要 $\Theta(|V|)$ ，由上面的式子可得，最终的时间复杂度还是 $\Theta(|V|^2)$ 。
使用邻接表，先直接给出结论：$O(|V|ln(|V|) + |E|ln(|V|))=O(|E|ln(|V|))$ 。

如果我们使用邻接表并且搭配优先队列（堆），来使用，那就有可能做到更快。上面的结论可以先记住，需要搭配后面代码来理解。

  
#include <iostream>
#include <vector>
#include <queue>
#include <climits> // 用于 INT_MAX

using namespace std;

const int INF = INT_MAX;

// 定义一个别名，pair<int, int> 用于存储 {权重, 顶点}
typedef pair<int, int> iPair;

// 图的类定义
class Graph {
    int V; // 顶点数量
    // 邻接表实现：adj[u] 包含多个 pair {v, weight}，表示 u -> v 权重为 weight
    vector<vector<pair<int, int>>> adj;
public:
    Graph(int V) { // 构造函数
        this->V = V;
        adj.resize(V);
    }
    
    // 添加无向边
    void addEdge(int u, int v, int weight) {
        adj[u].push_back({v, weight});
        adj[v].push_back({u, weight}); // 无向图需双向添加
    }
    
    // Prim算法核心实现
    void primMST() {
        // 1. 优先队列（最小堆）：存储 {当前最小权重, 目标顶点}
        // greater<PII> 确保队首是权重最小的元素，这和 C++STL 中 priority_queue 的实现有关
        // priority_queue<Type, Container, Functional>，Functional 即排序方式
        priority_queue<iPair, vector<iPair>, greater<iPair>> pq;

        // 2. 距离数组 (key/distance)：存储从 MST 到该顶点的最小边权
        // 初始化为无穷大
        vector<int> key(V, INF);

        // 3. 父节点数组 (parent)：用于记录 MST 的结构（边的来源）
        vector<int> parent(V, -1);

        // 4. 访问标记数组 (visited)：记录顶点是否已加入 MST
        vector<bool> inMST(V, false);

        // --- 初始化起始点 ---（存疑）
        int src = 1; // 从顶点 1 开始（可以任意选择）
        pq.push({0, src}); // 将起点入队，权重设为 0
        key[src] = 0;      // 起点到 MST 的距离为 0

        int totalWeight = 0; // 记录 MST 总权重
        int edgeCount = -1; // 记录加入的边的数量

        // --- 主循环 ---
        while (!pq.empty() && edgeCount < V - 1) {
            // 取出当前距离 MST 最近的顶点
            int u = pq.top().second;
            pq.pop();

            // 如果 u 已经在 MST 中，说明堆中这个元素已被访问，直接跳过
            // 需要注意，而由于STL中优先队列的限制，我们无法将旧的边权重更新或删除，
            // 采用的是只增不减的方法，所以可能会有多余的边堆积。
            // 但是我们设置了 while 的循环次数之后可以避免这个问题，另一个方法就是使用
            // 下面这行的方法来直接规避冗余边。
            // 其实可以不要这步，因为循环已经限制了次数，不会让同一节点的冗余边产生影响
            if (inMST[u]) continue;

            // 将 u 正式加入 MST
            inMST[u] = true;
            totalWeight += key[u]; // 累加权重 (对于起点是+0)
            edgeCount++;

            // --- 检查 u 的所有邻接点 v ---
            for (auto& edge : adj[u]) {
                int v = edge.first;
                int weight = edge.second;

                // 如果 v 还没在 MST 中，且通过 u 连接 v 的权重比 v 当前记录的权重更小
                if (!inMST[v] && weight < key[v]) {
                    // 更新 v 的最小权重
                    key[v] = weight;
                    // 记录 v 的父节点是 u
                    parent[v] = u;
                    // 将新的 {权重, 顶点} 入队
                    // 将权重放在前，因为 STL 优先队列默认第一个元素排序
                    pq.push({key[v], v});
                }
            }
        }
        
        // 5. 结果检查
        if (edgeCount < V - 1) {
            cout << "\n错误：图不连通！无法生成单一的最小生成树。" << endl;
        } else {
            cout << "\n最小生成树构建完成，总权重: " << totalWeight << endl;
        }
    }
};

while 到 for 循环之前：

  
while (!pq.empty() && edgeCount < V - 1) {
            // 取出当前距离 MST 最近的顶点
            int u = pq.top().second;
            pq.pop();
            
            inMST[u] = true;
            totalWeight += key[u];
            edgeCount++;

通过堆来寻找最小的边时，时间花费出现在 pq.pop(); ，需要 $O(ln(|E|))$ 的时间。在最坏情况下，边的数量是 $|E|=O(|V|^2)$ ，那么就是 $O(ln(|V|))$ 的时间。在主循环中，总共遍历 $|V|-1$ 次，这一步花费 $O(|V|ln(|V|))$ 的时间。

for 循环中：

  
for (auto& edge : adj[u]) {
    int v = edge.first;
    int weight = edge.second;

    // 如果 v 还没在 MST 中，且通过 u 连接 v 的权重比 v 当前记录的权重更小
    if (!inMST[v] && weight < key[v]) {
        key[v] = weight;
        parent[v] = u;
        pq.push({key[v], v});
    }
}

检查新加入节点的邻居节点时，时间花费出现在 if 判断中 pq.push({key[v], v}); 每一次 push 同样需要 $O(ln(|V|))$ 的时间。

在 while 主循环中，因为使用的是邻接链表，每次都要将新加入节点的所有邻接节点边 push 进去再进行判断和更新，也就是 $|E|$ ，每一次 push 同样需要 $O(ln(|V|))$ 的时间。总共就是 $O(|E|ln(|V|))$ 。

$|E|$ 最小也是 $|V|-1$ ，所以 $|E|$ 通常是更大的，即最终：$O(|V|ln(|V|) + |E|ln(|V|))=O(|E|ln(|V|))$ 。

Kruskal 算法构建最小生成树

最小生成树需要边的权重尽可能小，所以 Kruskal 算法给出了这样的实现：P178

先将图中的所有边从小到大进行排序；
依次取出每个边，如果没有和当前构建的MST产生回路，那么就添加进MST；
直到最后走完所有的边就结束。

Kruskal 算法的时间复杂度由两部分组成：排序时间+是否成环检测时间

首先需要使用快排等排序算法将所有边根据权重进行排序，花费 $O(|E|ln(|E|))$ 的时间。$|E|=O(|V|^2)$ ，即 $O(|E|ln(|V|))$ 。
从小到大每次取出当前最短边（$O(|E|)$），还需要判断是否存在回路，即需要遍历全部点($O(|V|)$)，花费时间 $O(|E||V|)$。

总时间为：$O(|E|ln(|V|))+O(|E||V|)=O(|E||V|)$。

我们发现，在判断回路这里花费了很多的时间，那么考虑一下有什么方法能加快？

不断向MST添加边这个行为和向一个集合中添加元素很像；
判断是否产生回路和查找元素是否在一个集合中是一样的 find(a) ；
添加的边将两个节点/不同区域的MST相连，和并查集中 set_union 很像；

因此我们可以使用并查集（Disjoint Set） 的方法来优化，这样加快了MST中是否有回路的判断速度。模拟过程 P205-217 。

具体的代码实现：

  
// BY Gemini 3 pro
// Kruskal 算法主函数
// V: 顶点数量, edges: 边的列表
int kruskal(int V, vector<Edge>& edges) {
    // 1. 排序：将所有边按权重从小到大排序
    // 时间复杂度：O(E log E) 或 O(E log V) 
    sort(edges.begin(), edges.end());

    // 2. 初始化并查集
    // 并查集类 (Disjoint Set Union - DSU)
    DSU dsu(V);

    int mstWeight = 0; // 最小生成树总权重
    int edgesCount = 0; // 记录已加入 MST 的边数

    // 3. 遍历排序后的边
    for (const auto& edge : edges) {
        // 尝试合并边的两个顶点
        // unite 函数内部调用 find 判断是否在同一集合（查环）
        // 如果不在同一集合，则合并并返回 true；否则返回 false
        if (dsu.unite(edge.u, edge.v)) {
            mstWeight += edge.weight;
            edgesCount++;
        }
        // 这里可以进行优化：根据树的性质，MST 一定包含 V-1 条边
        // 如果已经找到了 V-1 条边，可以提前结束循环
        if (edgesCount == V - 1) {
            break;
        }
    }
    // 如果边数小于 V-1，说明图不连通
    if (edgesCount < V - 1) {
        cout << "警告：图不连通，生成的是最小生成森林而非生成树。" << endl;
        return -1; 
    }
    return mstWeight;
}

并查集优化后，时间复杂度由：排序时间+并查集是否成环检测时间 组成。

排序时间仍和前面结果一样，$O(|E| \ln |E|)$，$|E|=O(|V|^2)$，即最后 $O(|E| \ln |V|)$。

并查集检测是否成环：检测成环需要对每条边 $|E|$ 做 find 和可能的 set_union 操作，每次操作耗时 $\Theta(\alpha(|V|))$ 。由于实际应用中可以看成 $\alpha(|V|) = \Theta(1)$ ，这部分时间花费就是 $O(|E| \cdot \alpha(|V|)) \approx O(|E|)$ 。

这样时间复杂度就降低为 $O(|E| \ln |V|)+ O(|E| \cdot \Theta(1))=O(|E|ln(|V|))$ 。

最短路径

在一个有权重的图中，还经常考虑这个图中两点间的最短的路径是什么样的？

Dijkstra 最短路径算法

在最短路径的寻找中，我们需要关注的不再是当前状态下哪个邻接节点的边是最短的，我们需要考虑从出发点一直到现在时哪条路径是最短的。

假设边的权重都是正整数；

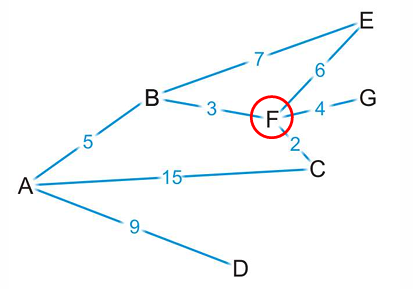
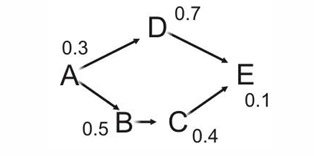
我们现在先从A出发，挑选最短的路径，到了B；

然后在从B往后走，此时如果到F，从A出发的路径长度为8，仍旧是目前最短的（小于AD=9）;

但是如果从F继续往后走，我们选择走到在邻接节点中更近的C，此时从A出发的路径长度就是10，大于从A直接到D的路径长度9。因此现在来说，从A到D应该是更短的一条路。

我们会发现，Dijkstra 算法和Prim算法的实现其实很像，

开始时都不知道除了起始点之外的边信息；
需要不断接入距离最近的边并更新邻接节点来确定下一步；

不同的点在于：

在检查邻接节点的距离时，最小生成树Prim算法只关注邻接节点中到新接入的这个节点最近（且未被访问过）的是谁？

而Dijkstra算法需要考虑从出发点一直到现在的路径长度，即接入哪个邻接节点可以使当前走过的全部路径最短？

具体模拟和Prim及其相像，P251-284 。

我们只需要修改Prim算法中的两处代码即可：

  
// Prim 算法判断邻接节点
for (auto& edge : adj[u]) {
    int v = edge.first;
    int weight = edge.second;

    // 这里只关注邻接节点的距离是否最小
    if (!inMST[v] && weight < key[v]) {
        // 更新 v 的最小权重
        key[v] = weight;
        parent[v] = u;
        pq.push({key[v], v});
    }
}

// Dijkstra 算法判断邻接节点
for (auto& edge : adj[u]) {
    int v = edge.first;
    int weight = edge.second;

    // 这里关注：到这个邻接节点的整条路径长度是否最小
    // Dijkstra 中的 key 是从出发点到 v 的路径长度旧记录
    if (!inMST[v] && key[u] + weight < key[v]) {
        // 更新到 v 的累加距离
        key[v] = key[u] + weight;
        previous[v] = u;
        pq.push({key[v], v});
    }
}

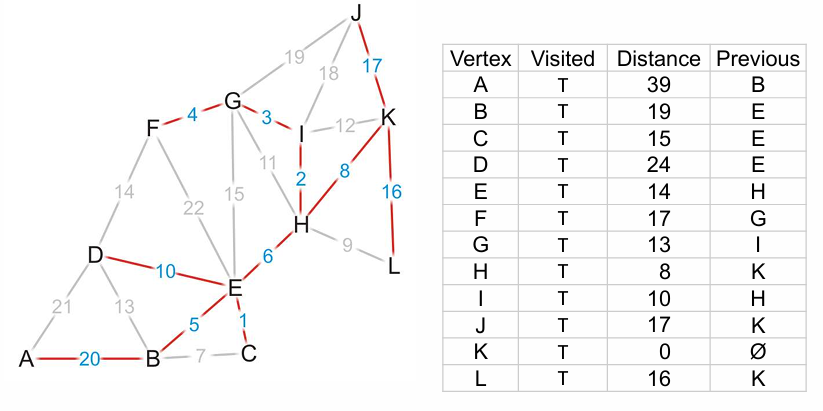
一旦我们找到了出发点（下图K）到每个节点的最短路径，只需要根据每个节点的 prevoius 回溯即可构建完整的最短路径。如果需要到特定节点，只需要判断找到节点停止即可。

时间复杂度和Prim没有区别：$O(|V|ln(|V|) + |E|ln(|V|))=O(|E|ln(|V|))$。

拓扑排序

拓扑排序是基于有向无环图（DAG）而来的。

一个DAG至少有一个入度为0的节点，拓扑排序基于每个节点的入度。

具体流程 P20-23 ，拓扑排序的结果不唯一。

如果每次我们都要通过遍历表格来找到入度为0的节点，那么无论采用什么方式都是 $O(|V|^2)$ 的时间复杂度。因此我们可以使用一个队列来存储入度为0的节点，免去寻找的耗时。

使用队列优化的算法实现： 模拟过程：P56-104

1、初始化：

先将图中所有节点的入度储存在表中；使用一个队列储存入度为0的节点；

2、迭代过程：（当队列不为空）

弹出队首顶点 $v$，将其加入拓扑排序结果序列。
遍历 $v$ 的所有邻接节点（即 $v$ 指向的顶点），将其邻接节点的入度 -1。
如果邻接节点的度为0，将其入队。

3、当队列为空时，遍历结束。

如果最后仍存在入度不为0的节点，那么就说明存在环路。

在使用队列时，可以进行一个简化（This is a trick）。对于这个储存in-degree为0的队列，每个顶点仅进出队列一次，耗时 $\Theta(|V|)$ 且该队列最多只有 $|V|$ 个元素。

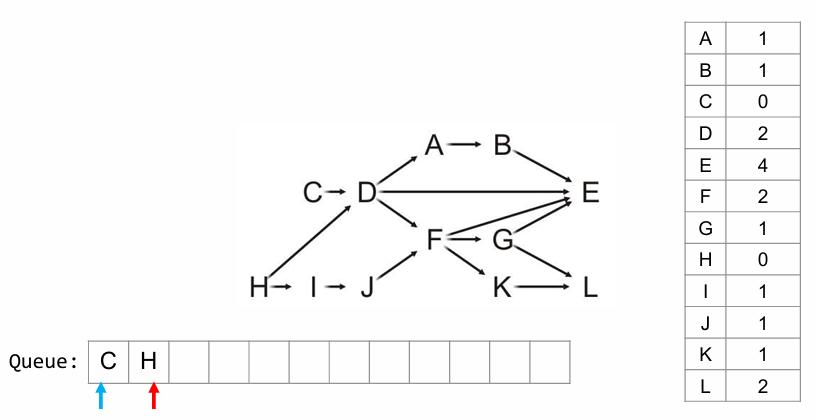
所以我们可以直接申请一个大小为 $|V|$ 的数组，然后使用两个指针ihead（队头）和 itail（队尾）来向后处理，避免了动态内存分配和频繁调整大小。并且也不需要像队列一样再弹出，移位之类的操作。

如图即为将C、H入队后的情况，蓝色为ihead，红色为 itail ，从队尾入队。

最终得到的这个队列就是拓扑排序的结果。

使用邻接链表实现时，初始化时需要遍历完每一个节点+队列弹出入度为0的节点时，需要走过每一个节点实际拥有的邻接节点，和边 $|E|$ 有关。时间复杂度：$\Theta(|V| + |E|)$ 。

使用邻接矩阵实现时，时间花费由弹出队列节点后查询邻接节点主导，找到某个节点的邻接节点需要 $\Theta(|V|)$ ，全部节点都过一遍，即：$\Theta(|V|^2)$ 。

用于储存的表格需要 $\Theta(|V|)$ 空间复杂度。

任务管理和关键路径Critical Path

一个DAG还可以用于项目管理和任务调度，因为他能告诉我们哪些任务是可以并行的，哪些任务是相互关联的。

对于一个整体项目的开展，我们希望能知道他们之间的相互依赖会怎么影响整个项目的工作时间，也就是：在一个前后依赖（可能存在并行）的任务组中，完成所有任务所需的最短时间是多少？

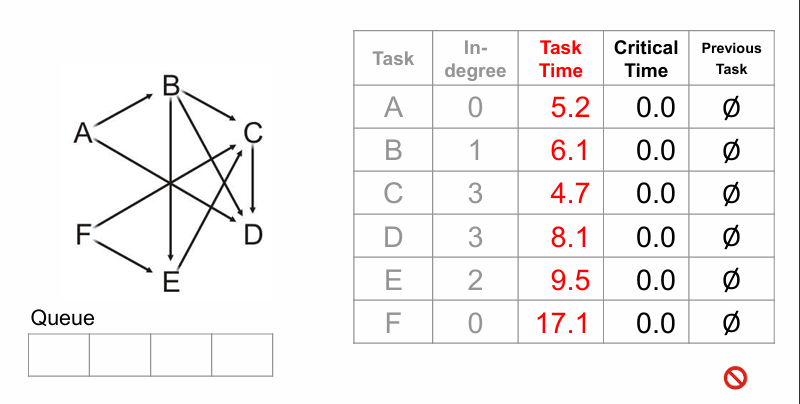
在这个图中，我们可以看到，从A到E需要完成全部任务需要的时间应该是1.3而不是1.1，因为走底下的这条路（ABCE）花的时间更久，上面的路（ADE）虽然时间短但是为了整个任务的完成，需要等待下面的完成。

所以，完成任务的最短时间也可以理解为：

完成这个任务，从头到尾，影响最大、最关键的是哪一条路？

在寻找这个影响最大的关键路径（Critical Path） 之前，我们需要知道一些信息：

完成每一个独立任务需要的时间，图中每个节点的时间；
完成这个任务的关键时间（Critical Time） ，初始化为0；
该任务之前关键时间最长的关键路径是哪一条；

像之前一样，可以使用多个列表构建起一个表格：

具体算法流程是：

和in-degree节点相关的操作同前。
每次我们从记录in-degree为0的队列中弹出一个节点 $v$ 时，计算他当前的关键时间（他前面的关键时间+自己的时间）；
对于节点 $v$ 的所有邻接节点 $u$ ，如果 $v$ 的关键时间比 $u$ 现在的关键时间要长，那么更新 $u$ 的关键时间为 $v$ 的关键时间；且将其 previous task 设置为 $v$ 。

流程模拟 P113-138

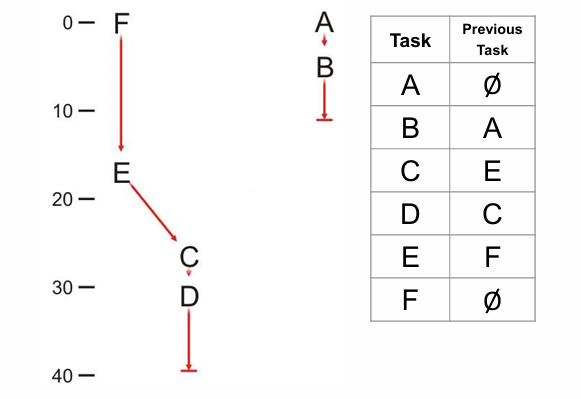
最终我们可以通过表格中的 previous task 来反推出整个DAG是什么样的，从中我们可以清晰地看到这个流程中的关键路径和可并行的任务。

数据结构, 课程笔记

本文由作者按照 CC BY 4.0 进行授权