桶排序Bucketsort和基数排序Radixsort

在学习完Mergesort和Quicksort之后，我们会发现他们的时间复杂度似乎已经突破不了 $\Theta(nln(n))$ ，这其实是这类排序算法的局限。

这类排序算法的本质其实是通过元素间的移动、交换来最终实现排序。理论已经证明了基于元素交换的排序算法存在速度上限 $\Theta(nln(n))$ ，因此我们无法尝试再去在元素交换的基础上去提高速度。

能不能换种方法继续提高速度？

答案是可以的，但是我们必须要牺牲算法的适用性。当我们给某个排序算法做出一些假设时，可以更加快速的实现排序。

桶排序Bucketsort

假设数据（如整数）落在某个已知的特定范围内，然后我们为这个范围内可能存在的数据都创建一个bucket（桶），用于储存 bit 值（0 or 1）。整个数据存储为一个 bitsVector

具体的排序流程： P355

• 根据数据范围创建每个值对应的桶；
• 过一遍数据，并在对应的桶（索引）进行标注，通过位运算将相应位置设置为1；
• 然后遍历所有桶，输出存在的值，完成排序；

但是这样还存在一个严重的问题，简单的位向量（每个桶只能表示“有”或“没有”）无法正确处理重复项。

那么将其改进为 Countingsort，计数排序。每个桶添加：

• 一个计数器
• 一个链表 计数器用于记录该数据的数量，链表则可以更加准确的区分这些重复元素（如区分 $a_1,a_2,a_3 = 1$ ）

通过这样简单的两个过程就实现了排序，这两个算法的时间复杂度都是 $\Theta(n+m)$ 。 $n$ 是元素个数，$m$ 是创建的桶的数量（即数据范围）（过一遍已有数据+遍历所有桶）

但是对于Bucketsort，$m$ 不可能小于 $n$，因为不允许有重复项。

并且对于桶排序，通常要求数据分布比较均匀和稠密，因为他是根据数据范围来创建的； 试想一下：排序一个电话号码 [0,1,2,100000000] ，这样岂不是要创建0-10000000个桶？这对空间的占用和浪费是非常巨大的。

基数排序 (Radix Sort)

如果直接对 10 位数字使用桶排序，将需要 $10^{10}$ 个桶，这在内存上（约 9 GiB）是不切实际的，而基数排序则通过逐位进行桶排序来解决这个问题。

流程： P372 例子

• 创建 $k$ 个队列（桶），$k$ 是基数（例如，十进制为 10，二进制为 2）；
• 从最低位开始向上迭代（从个位开始）；
• 每次迭代都是直接对当前位使用桶排序，按顺序输出一个新的列表；
• 重复直到处理完最高位；

为什么可以这样做？

• 队列保证了当前位一样的元素都可以被放进桶中，每个队列都要有 $n$ 个位置；
• 如果当前位的数不一样（例如 $a_i < b_i$），那么在桶排序的作用下，$a$ 会被放入较低的桶中，因此会比 $b$ 先输出，新的输出列表相当于根据当前位被重新桶排序了；

为什么要从最低位开始？能不能从最高位开始？

必须从最低位开始！ 因为不断往上进位再桶排序的过程实际上是在寻找决定性的数位。 比如 309 和 209 进行比较，即使前两位相同，但是百位的 $3>2$ 彻底杀死比赛，桶排序时309一定比209靠后。如果从最高位开始往最低位走，那么如果两个数的各位不同（206，581），就会因为最后 $6>1$ 而导致206在581后。

基数排序的时间复杂度在全部情况下都是 $\Theta(n \ln(m))$ ，$n$ 的数据量，$m$ 数据范围（对于范围 $m$，位数大约是 $\log(m)$（例如 $\log_2(m)$ 或 $\log_{10}(m)$）），全部位都要走一遍。

十进制好还是二进制好？

• 十进制会浪费 $10n-n=9n$ 的空间；
• 二进制浪费 $2n-n=n$ 的空间； 二进制会更好。

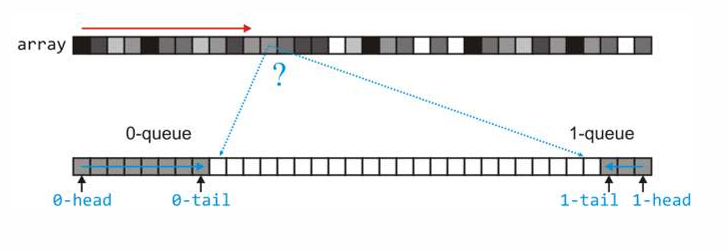
对于二进制来说，只有两个桶（队列），0和1；并且每个队列的位置都有 n 个。 但是这样还是会有 n 的空间被浪费，那么此时我们只需要将队列改为双端队列（Deque） 即可实现通过一个队列放置0和1的队列。