Hashing和哈希表
前面我们学习过在AVL树中,我们实现查找到叶子节点或者其他操作的时间受到树高 $O(\log N)$ 的限制,现在我们再来看看有没有更快的一种搜索并查找我们想要的数据。
Map ADT
首先来看看一种新的ADT,Map,映射。
一个映射是一个或多个键值对 (Key, Value) 的集合,对于每一个键值对,Key是唯一的。 支持两个操作:
get(key):获取键对应的值put(key, value):插入或更新键值对
Hash Table 哈希表
在哈希表 (Hash Table) 中,通过哈希函数将键映射为一个哈希值(通常是数组索引)来实现 $O(1)$ 时间的查找访问。
我们先定义:
- 一个哈希表(数组)的长度为 $TableSize$ ;
- 对应的哈希函数
hash(key),来将一个整数映射到范围为[0,TableSize-1]的数组索引中。
对于整数值key
为了使key能映射到整个table的范围当中,最简单情况下通常采用这样的哈希函数:
1
2
3
int hash( int key, int tableSize ) {
return key % tableSize;
}
在整数值key的情况当中,理想的情况是均匀随机分布,这样能尽可能保证表单元能被使用。
对于字符串key
可以通过 ASCII 来转换为整数表示,我们一般有三种哈希函数的设计方法:
- 第一种:将字符串中的全部字符
ASCII值相加求和
这种办法最简单,但是也有一个致命的问题,非常容易出现 Collisions,也就是两个键的映射重复(出现碰撞),例如:“rescued”,“secured”,“seducer”,这三个词 ASCII 码都是相同的。
并且当 TableSize 很大的时候,假设我们的字符串最多有8个字符,即使我们将他们最大的ASCII码字符全部加起来 $8*127+1(0的情况)=1017$ ,也最多使用1017个,浪费了很多空间。
- 第二种: 使用 $key[0] + 27 \cdot key[1] + 27^2 \cdot key[2]$
这种方法是借鉴了十进制数中的表示方法(在这里我们只考虑字符串类型,因此1并不是在百位,而是作为第 [0] 个值) $ 123 = 1 \times 10^0+2 \times 10^1+3 \times 10^2 $ ,但是这里只使用了3个字符,数据量小且比较便捷,但是当然也不可避免地会出现很多冲突。
同时,字符串key存储的通常是人名、物品名之类有规律的单词,几乎不会使用某些字符。因此也会造成存储浪费。
- 第三种: $key[N−1]⋅31^N+key[N−2]⋅31^{N−1}+⋯+key[1]⋅31+key[0]$
这是一种 java 语言在处理字符串时使用的哈希函数映射方式,有比较好的效果。 采用了多项式滚动的表示方法,和第二种类似,但是可以覆盖一个字符串的全部字符;
1
2
3
4
5
6
7
8
9
10
11
int hash( string key, int tableSize ) {
int hashVal = 0;
for( int i = 0; i < key.length( ); i++ )
hashVal = 31 * hashVal + key[i];
hashVal %= tableSize;
if( hashVal < 0 )
hashVal += tableSize;
return hashVal;
}
并且将底数从27改为了31,这是一个很重要的改动,从一个合数变为一个质数作为底数,是为了减小发生重合的可能。
当然这种采用火力覆盖的方式仍然会在数据量较大时占用巨大空间,导致执行速度变慢。
关于质数的参与
其实 TableSize 也需要尽可能使用质数,这样哈希函数在通过取模操作来进行映射时能降低余数出现重合(碰撞)的可能性。(这里主要和数论有关)
“为了减少重合,TableSize 不应该(在取模之前)成为任何一个较大的哈希值的因数。”
这句话中的“哈希值”可能会产生一点误解:在很多哈希函数映射过程中,会产生多个中间哈希值,而为了使哈希值落在 TableSize 的范围内,需要一直取模。在这个过程中,如果是因数,那么就会产生周期性,最终导致多个key的哈希值相同而产生碰撞。
例如:TableSize=8,那么会有非常多偶数的哈希映射结果为:0,2,4,6 而产生大量冲突。
在上面的内容中,多次出现了“碰撞”这个词,其实这也是哈希表需要解决的最大问题,因为我们必须要保证哈希映射时总是一一对应(也可以对应“单射 one-to-one”) 的。
接下来将讨论多个 Hash Table Collisions 的解决办法。
Hash Table Collisions Solutions(一些解决办法)
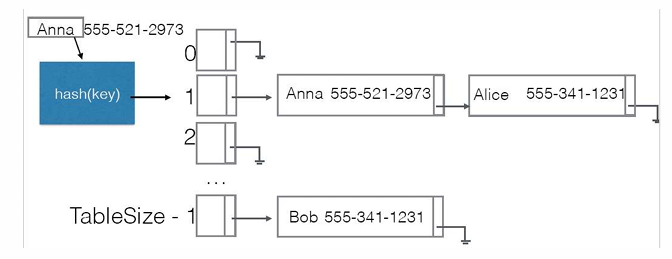
Separate Chaining(分散链式) P26
分散链式的思想很简单,就是将 key hash到一个桶 bucket 上,哈希值(bucket)重复的元素在这个 bucket处形成一个链表来存储,需要注意添加新的元素到这个链表的后面时使用的方法是 prepend ,前向添加。
寻找这个 key 需要的时间是:hash + 链表中的遍历查找。假设哈希函数计算需要 $O(1)$ 的时间,那么在后续链表中的查找需要多少时间呢?
这里我们给出一个参数:负载因数(Load Factor)\(\lambda=\frac{N}{TableSize}\) $N$ 是key的数量,$\lambda$ 表示了后续链表的平均长度。 查找过程:
- 将一个key hash到一个桶中,在这个桶中查找这个key是否存在?
- 如果不存在,那么这个key对应的键值对就不存在;
- 如果存在,那么取出这个键值对。
最终的设计目标就是尽可能地使 $\lambda=1$ ,这样哈希函数的映射就是 $O(1)$ 的,从而使得整个查找都是 $O(1)$ 的。
这个方法的缺点是需要额外的空间来存储对应的链表,并且相关链表的实现也需要大量的代码实现。
如果不使用链表呢?
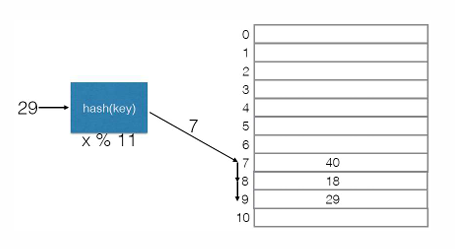
Probing(探针检测) P33
当我们将一个key hash后,哈希值发生碰撞,那么就移动到这个哈希值(索引)后面的某个空位置。
这种方式就是 Probing(探针检测),我们可以用一个公式来表示: \((hash(x)+f(i))\%TableSize\)
Linear Probing
如果这里 $f(i)=i$ 是一个线性函数,用来表示第 $i$ 次重复时后移 $i$ 个,即为”Linear Probing”。
如果要查找一个 key,就要从这个key一开始被hash到的hash值来查找。因此这样的方法会使哈希值形成一簇一簇的样子。
但这样的探针检测方式会在数据量越来越大时产生很大的cluster,很像在hash表中建了一个链表。在后面需要寻找空的hash位置时极为困难。
Quadratic Probing
那么这时候我们再考虑使用二次函数 $f(i)=i^2$ ,即 Quadratic Probing。P50
二次探针很好地解决了成簇的问题,仍然要求 TableSize 需要是质数来避免出现碰撞,但此时是有空闲的hash值位置。并且如果 $\lambda>0.5$ ,那么即使有空位且 TableSize 为质数,也很难再成功放入。
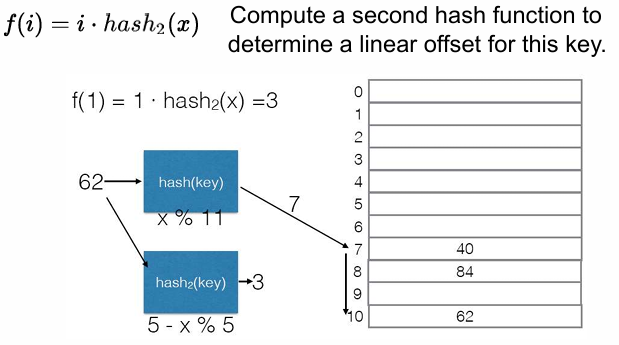
二次哈希(Double Hashing)
再考虑变形:$f(i)=i\cdot hash_2(x)$ 来使用二次哈希进行相同 hash 值的计算与偏移。P60
对于这个二次哈希函数的选择我们需要非常的谨慎!否则可能出现重复的永远映射到同一个地方! 对于整数的 hashing,比较好的是 $hash_2(x)=R-(x\%R)$ ,只要设计合理,二次哈希能带来相对最好的 key 的分布。
一般来说,当我们进行了大于 $\frac{TableSize}{2}$ 的 insert 后,就需要对哈希表进行 Rehashing,重哈希。
注意,由于 hashing 是基于 $TableSize$ 的,因此 rehash 时不能简单地平移或者不动,而是需要基于新的 $TableSize$ 重新 hashing,Rehashing需要 $O(n)$ 的时间。